Производственная функция

ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ - функция, отображающая зависимость между максимальным объемом производимого продукта и физическим объемом факторов производства при данном уровне технических знаний.

Поскольку объем производства зависит от объема использованных ресурсов, то зависимость между ними может быть выражена в виде следующей функциональной записи:

Q = f(L,K,M),

где Q - максимальный объем продукции, произведенной при данной технологии и определенных факторах производства;

L - труд; К - капитал; М - материалы; f - функция.

Производственная функция при данной технологии обладает свойствами, которые определяют соотношение между объемом производства и количеством используемых факторов. Для разных видов производства производственные функции различны, тем не менее все они имеют общие свойства. Можно выделить два основных свойства.

1. Существует предел для роста объема выпуска, который может быть достигнут ростом затрат одного ресурса при прочих равных условиях. Так, в фирме при фиксированном количестве машин и производственных помещений имеется предел роста выпуска путем увеличения дополнительных рабочих, поскольку рабочий не будет обеспечен машинами для работы.
2. Существует определенная взаимная дополняемость (комплектарность) факторов производства, однако без уменьшения объема выпуска вероятна и определенная взаимозаменяемость данных факторов производства. Так, для выпуска блага могут быть использованы различные комбинации ресурсов; можно произвести это благо при использовании меньшего объема капитала и большего объема затрат труда, и наоборот. В первом случае производство считается технически эффективным в сравнении со вторым случаем. Однако существует предел того, насколько труд может быть заменен большим объемом капитала, чтобы не сократилось производство. С другой стороны, имеется предел применения ручного труда без использования машин.

В графической форме каждый вид производства может быть представлен точкой, координаты которой характеризуют минимально необходимые для выпуска данного объема продукции ресурсы, а производственная функция - линией изокванты.

Рассмотрев производственную функцию фирмы, перейдем к характеристике следующих трех важных понятий: общего (совокупного), среднего и предельного продукта.

На рис. 22.1, а показана кривая общего продукта (ТР), который изменяется в зависимости от величины переменного фактора X. На кривой ТР отмечены три точки: В - точка перегиба, С - точка, которая принадлежит касательной, совпадающей с линией, соединяющей данную точку с началом координат, D - точка максимального значения ТР. Точка А перемещается по кривой ТР. Соединив точку А с началом координат, получим линию ОА. Опустив перпендикуляр из точки А на ось абсцисс, получим треугольник ОАМ, где tg а есть отношение стороны AM к ОМ, т. е. выражение среднего продукта (АР).

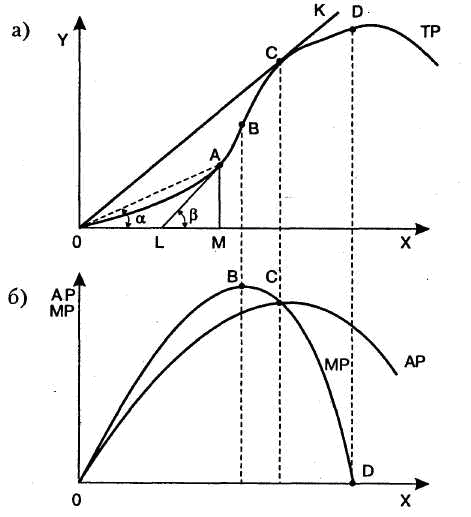
Рис. 22.1. а) Кривая общего продукта (ТР); б) кривая среднего продукта (АР) и предельного продукта (МР)

Проведя через точку А касательную, получим угол Р, тангенс которого будет выражать предельный продукт МР. Сопоставляя треугольники LAM и ОАМ, находим, что до определенного момента тангенс Р по величине больше tg а. Таким образом, предельный продукт (МР) больше среднего продукта (АР). В том случае, когда точка А совпадает с точкой В, тангенс Р принимает максимальное значение и, следовательно, предельный продукт (МР) достигает наибольшего объема. Если точка А совпадает с точкой С, то значение среднего и предельного продукта равны. Предельный продукт (МР), достигнув максимального значения в точке В (рис. 22, б), начинает Сокращаться и в точке С пересечется с графиком среднего продукта (АР), который в этой точке достигает максимального значения. Затем и предельный, и средний продукт сокращаются, но предельный продукт уменьшается опережающими темпами. В точке максимума общего продукта (ТР) предельный продукт МР = 0.

Мы видим, что наиболее эффективное изменение переменного фактора X наблюдается на отрезке от точки В до точки С. Здесь предельный продукт (МР), достигнув своего максимального значения, начинает уменьшаться, средний продукт (АР) еще увеличивается, общий продукт (ТР) получает наибольший прирост.

Г.C. Beчкaнoв, Г.P. Beчкaнoвa

Другие материалы по теме Производственная функция

Микроэкономика...